D* Lite算法是一种增量启发式搜素算法,由Sven Koeing和Maxim Likhachev于2004年提出,是基于LPA* 和Dynamic SWSF-FP的一种算法。D* Lite算法可以适用于地图未知、环境随时会发生变化的情况,在遇到新增加的障碍物时,可以利用先前搜索所获得的信息,而不需要完全重新规划路径。
基础算法介绍
在介绍D* Lite之前先简单介绍下广度优先、最佳优先以及A* 算法。如果要在一个网格地图中找到两点之间的最短路径,很容易想到的广度优先算法和最佳优先算法。
这章用的图片都来自于这篇博客:https://paul.pub/a-star-algorithm/。这篇博客对A* 算法对介绍也非常详细。
广度优先算法
广度优先算法就是从一个点开始遍历周围的节点,逐步向外扩散,已经遍历过的就不用再遍历,直到找到了终点。就如下图所示:

广度优先算法的优点是一定可以找到两点间的最优路径,但是代价就是需要搜索的点非常多,速度会比较慢。
最佳优先算法
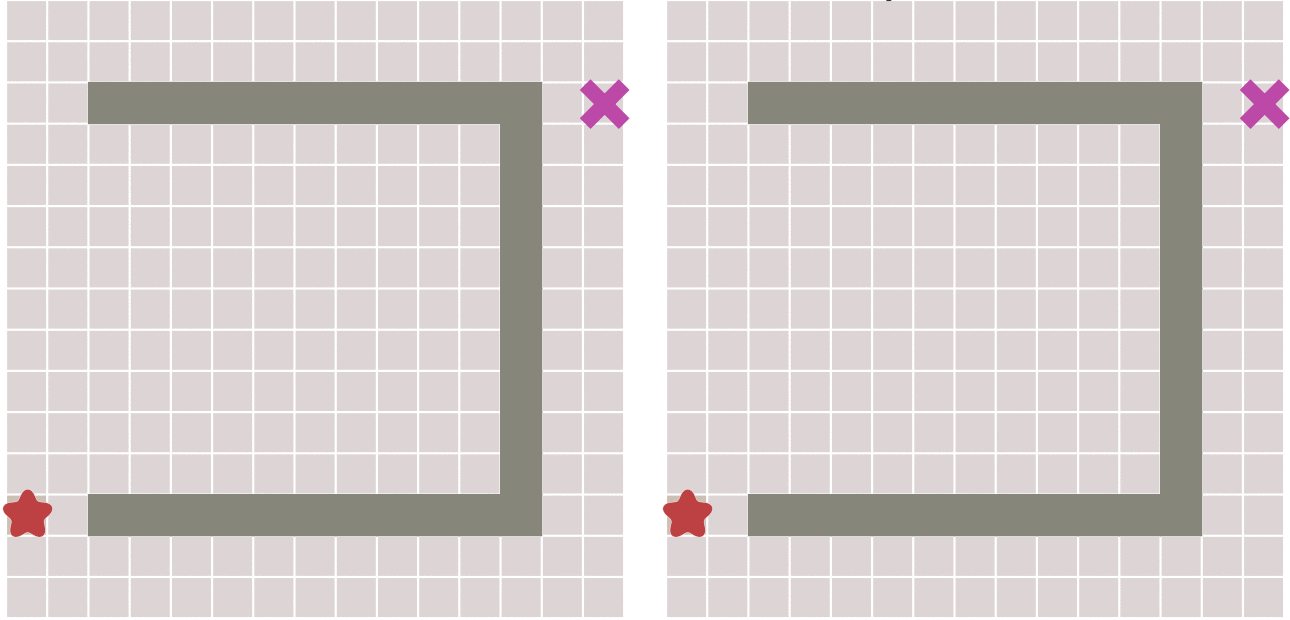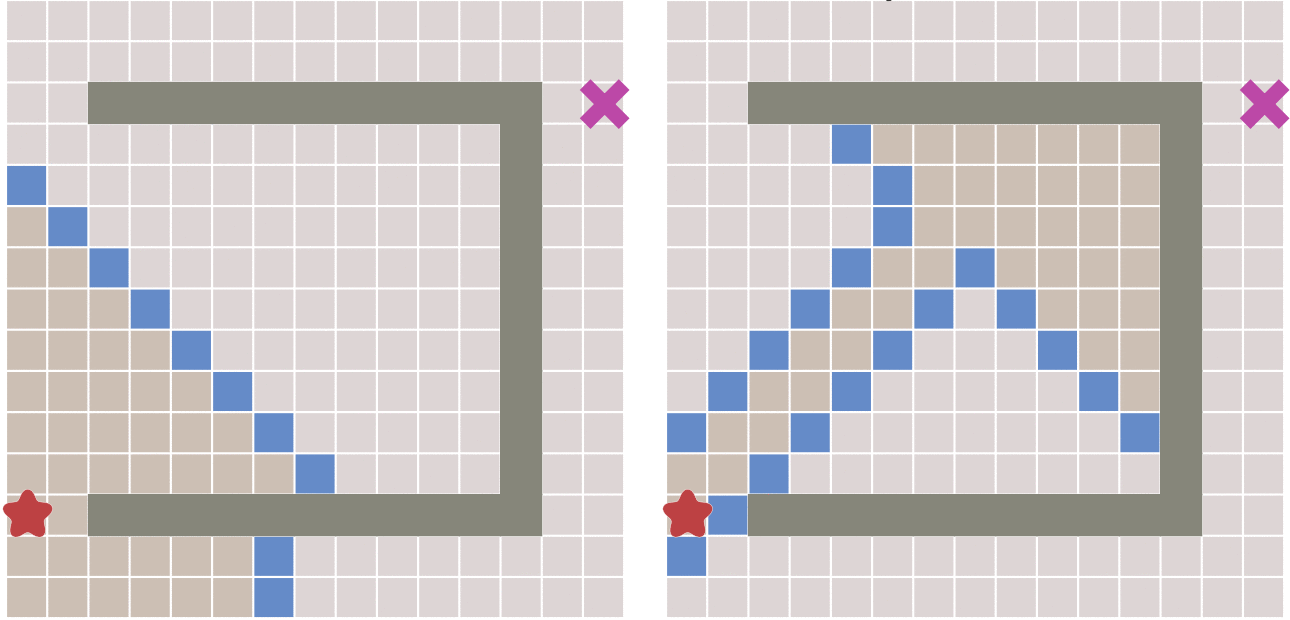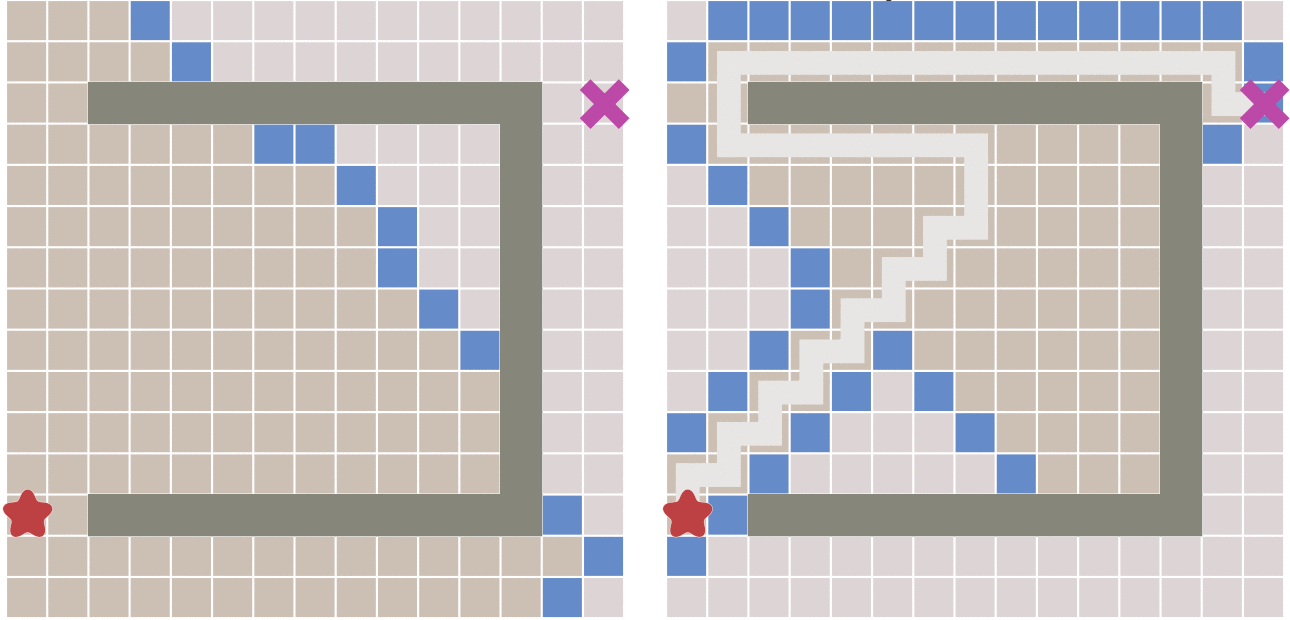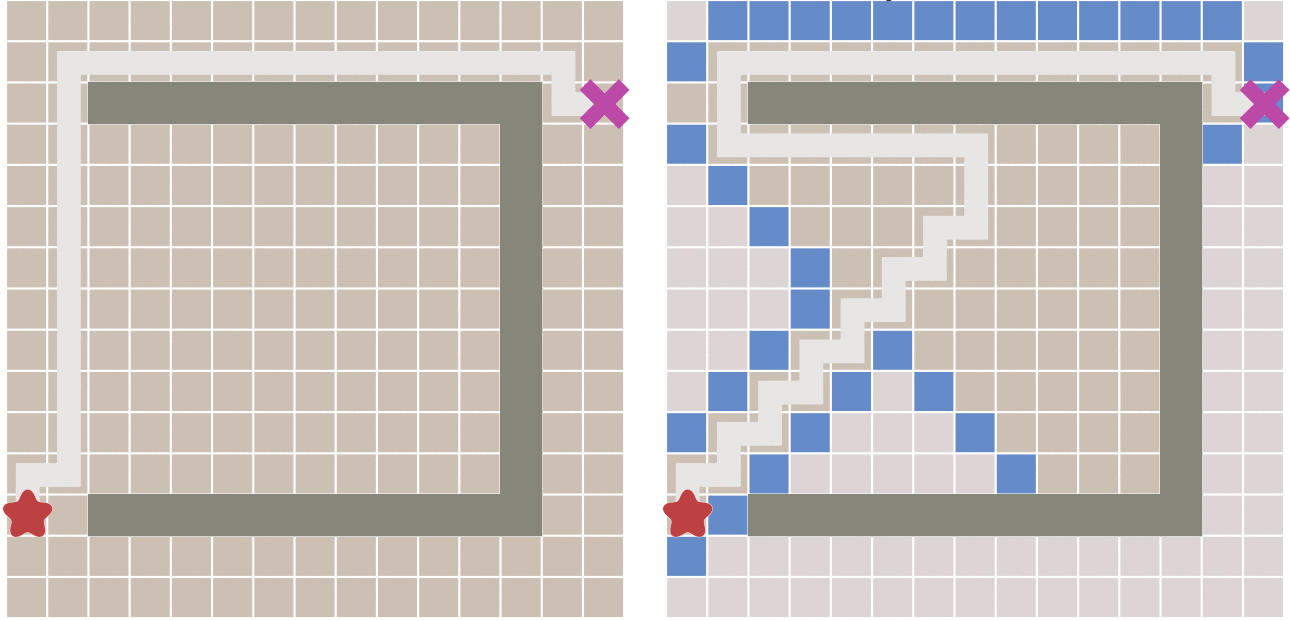
最佳优先算法和广度优先算法不同,它需要使用一个优先队列,用每个点到终点到距离到估计值来判断一个点的优先级。首先先遍历起点周围的点,计算到终点的距离,距离越近优先级越高。之后就取出优先队列中优先级最高的点,再遍历它点周围节点加入优先队列。之后就不断重复这个过程,直到到达终点。和广度优先相比,最佳优先所需要搜索的点要少很多,如下图所示:
但最佳优先算法的缺点就是,当起点和终点有障碍物时,可能最佳优先算法找到的路径并不是最佳的路径:
A*算法介绍
A* 算法就是把广度优先算法和最佳优先算法的优点所结合起来了。A* 算法通过下面的公式来评估一个点的优先级:
$$ f(n)=g(n)+h(n) $$
其中:
- f(n)是节点n的优先级评估值,f(n)值越小的点优先值越高。
- g(n)是节点到起点到实际代价。
- h(n)是启发函数,是节点n到终点到估计值。
A* 算法还需要使用两个集合来表示代遍历的节点和已经遍历的节点,通常成为open list和close list,其中open list需要使用优先队列。A* 算法首先从起点开始,计算周围的点的优先值并且加入优先队列。之后开始从优先队列中选取优先值最小的点,将其加入close list并且同样计算周围的点的优先值加入优先队列(close list中的点就不需要再计算了)。不断重复这个过程直到搜索到终点算法就结束,返回路径。
A* 算法的公式中,g(n)使得算法能选取相对来说走得更少的点,h(n)能使算法优先选择离终点更近的点(不考虑障碍物的情况,因为是估计值)。
D* Lite算法详解
D* Lite是一种增量启发式算法。启发式和A*类似,同样有一个启发函数,不过因为D* Lite是从终点向起点搜索,所以对应的启发函数h(n)也变成了节点n到起点的估计值。增量式算法之前找了好久也没有找到相关的定义,后来无意中在西瓜书里面看到了一段对增量学习对定义:
增量学习是指在学得模型后,再接收到训练样例时,仅需根据新样例对模型进行更新,不必重新训练整个模型,并且先前学得的有效信息不会被冲掉。
D* Lite算法就是这样,当检测到了新的障碍物,算法不需要完全重新规划路径,可以利用之前搜索所获得的信息,来找到一条可以避开障碍物的路径。
概念介绍
在介绍D* Lite的具体算法之前,先介绍几个它所引入的概念。
g值h值以及rhs值
和A* 不同,D* Lite是从终点向起点搜索,所以g(n)和h(n)的定义也就有所不同:
- g(n):当前点到终点的实际代价
- h(n):当前点到起点的估计值
D* Lite中引入了一个新的概念就是rhs(right-hand side),它的定义公式如下:
$$
rhs(s)=
\begin{cases}
0& if s=s_{goal}\\
min_{s’\in Pred(s)} (g(s’)+c(s’,s)) & \text{otherwise}
\end{cases}
$$
一个点的rhs值是它的父代节点中g值加上这两点之间的代价中的最小值,相当于一个点从父代节点到达这个点的最小代价。其实在算法的大部分过程中,g值和rhs值是相等的。具体rhs值的意义在后面再介绍。
两个key值
在A* 算法中,通过f(n)的大小来判断一个点的优先级,而在D* Lite中,需要通过两个key值来判断一个点的优先级,key值越小优先级越高,先判断第一个key值,如果第一个key值相等再判断第二个key值。它们的公式如下:
$$
k_1(s) = min(g(s),rhs(s))+h(s,s_{start})+k_m
$$
$$
k_2(s) = min(g(s),rhs(s))
$$
其中$k_m$的定义为,算法初始化时会先将$k_m$设置为0,之后当机器人有检测到地图的变化时,$k_m+=h(s_{last},s_{start})$,$s_{last}$代表的是上一个起点,$s_{start}$是机器人的当前位置。因为每当机器人有检测到地图的变化时,要计算两点之间的启发距离(不考虑障碍物),并且把当前所在的点设置为新的起点,即更新起点的位置。
我们一个个来看。首先是第一个key,它由三项构成,当前点的g值和rhs值中的最小值加上当前点到起点的估计值在加上一个$k_m$。简单的理解话:第一项就是到终点的实际距离,第二项是到起点的估计值,如果在机器人还没有移动的时候$k_m$就等于0,这时算法其实就相当于一个反向从终点往起点方向搜索的A* 算法了。那么$k_m$引入的意义是什么呢,当机器人检测到障碍的变化时会再一次规划路径,这时候的实际起点应该是机器人当前的位置,起点发生了变化,每个点的h值也会相应变化,key值也发生了变化。如果不引入这个参数的话,就需要把优先队列中的全部节点都重新计算一遍key值,增加了计算量。引入之后就可以一定程度上保证key值的一致性,减少计算量。
第二key值就是g值和rhs值中的最小值,它的意义在于当两个点的第一个key值相等的时候,算法会优先选择距离终点近的点。
局部一致性
D* Lite算法中还有一个很重要的概念就是局部一致性,通过一个点的局部一致性来判断当前点是否需要计算。其定义如下:当一个点的g值等于rhs值时称这个点为局部一致的点,否则称这个点为局部不一致。其中局部不一致的情况还可细分成为局部过一致和局部欠一致:当一个点的g值大于rhs值时,这个点为局部过一致,通常是有障碍物删除时或者算法第一次搜索路径时;当一个点的g值小于rhs值时,这个点为局部欠一致,通常是检测到了新增的障碍物。
算法伪代码理解
因为markdown写伪代码实在是不方便,所以这里就直接用论文里的图了。下面介绍论文伪代码中3个重要的函数
主函数

解释如下:
{29}首先是将机器人的当前点设置为起点。
{30}然后调用Initialize()函数进行初始化,初始化的内容如下:
初始化需要将优先队列设置为空队列;置为0;
将所有节点的g值和rhs值设置为无穷;
最后将终点的rhs值设置为0并计算它的key值加入到优先队列中。
{31}初始化之后就调用ComputeShortestPath()开始计算它的最短路径。
{32}~{48}之后就开始循环,直到机器人到达了终点。循环开始后:
{34}~{35}先根据之前的计算将机器人移动到子代中g值加上这两个点之间的代价中最小的点。
{36}~{48}如果机器人检测到了障碍的变化:
{38}~{39}修改k_m值,根据上一个起点和当前点的启发值,并且将当前点设置为上一个起点。
{40}对于所有两个点之间的代价发生变化的:
{41}~{42}另然后更新这两个点之间的代价
{43}~{44}如果:代表两个点之间的代价变小,有障碍物删除。那么优化它的rhs值。
{45}~{46}这里的判定条件是:代表原来的路径可以通过这两个点,但是他们之间的代价发生了变化,一般可以理解成可能的路径上新增了一个障碍物。然后再通过点的子代来更新rhs值
{47}更新受影响的节点
{48}计算最短路径
上面就是D* Lite的main函数,它的思路可以理解为先计算最短路径,其最短路径是通过周围点的g值来判断的,机器人一直走向g值加上两点代价最小的点。如果检测到了障碍物的变换,那么更新受影响点的rhs值,然后重新计算最短路径。
主函数的流程图如下: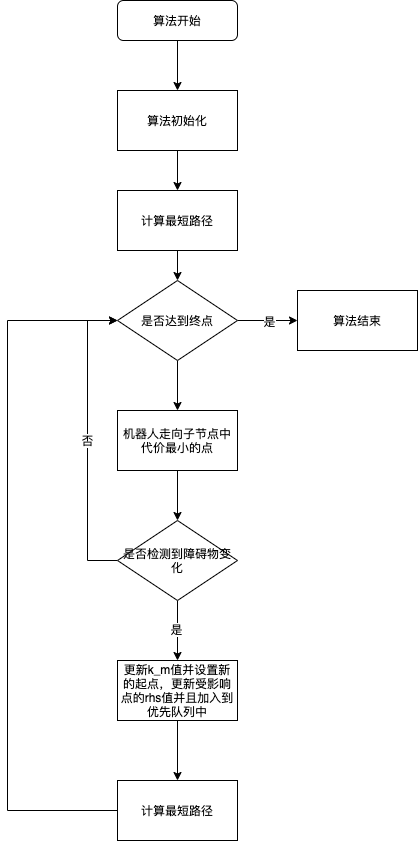
更新一个节点
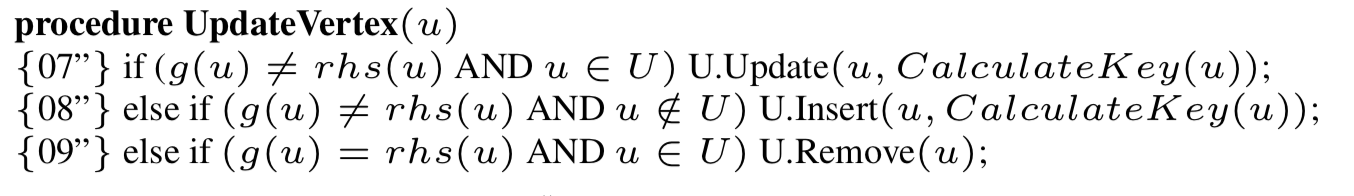
解释如下:
{07}如果当前点的g值和rhs值不相等,即为局部不一致,并且这个点在优先队列中,那么就更新这个点在优先队列中的key值。
{08}如果一个点的g值和rhs值不相等,并且这个点不在优先队列中,那么就计算这个点的key值,并加入到优先队列中。
{09}如果一个点g值和rhs值相等,并且还在优先队列中,那么就将其从优先队列中删除。
计算最短路径

解释如下:
{10}进行路径判断的条件是:优先队列中key值最小的key值要小于“起点”(机器人所在的位置)的key值或者起点的rhs值大于它的g值:
{11}~{13}取得优先队列中优先值最高即key值最小的节点和它的key值,并重新计算它的key值。
{14}~{15}如果它的新的key值大于它旧的key值那么就将它和它新的key值重新放到优先队列中。
{16}如果当前节点的g值大于rhs值(通常是第一次搜索或者有障碍物的删除时):
{17}~{18}另当前点的g值等于rhs值,并且将其从优先队列中移除。
{19}~{21}更新当前节点的父节点(且不是终点),如果可以让它们的rhs值取得更小的值,那么就更新它们的rhs值。最后调用UpdateVertex来将它们加入到优先队列中。
{22}否则(当前节点的g值小于等于rhs值,一般是有新增加的障碍物):
{23}~{24}记录当前节点的g值为之后将其置为无穷。
{25}对于所有的当前点的父节点以及当前点:
{26}~{28}如果它们({25}中的点)的rhs值等于加上两点间的代价,那么就从它的子节点来更新rhs值,最后再调用UpdateVertex来更新它们。
两个例子🌰
新增障碍物
删除障碍物
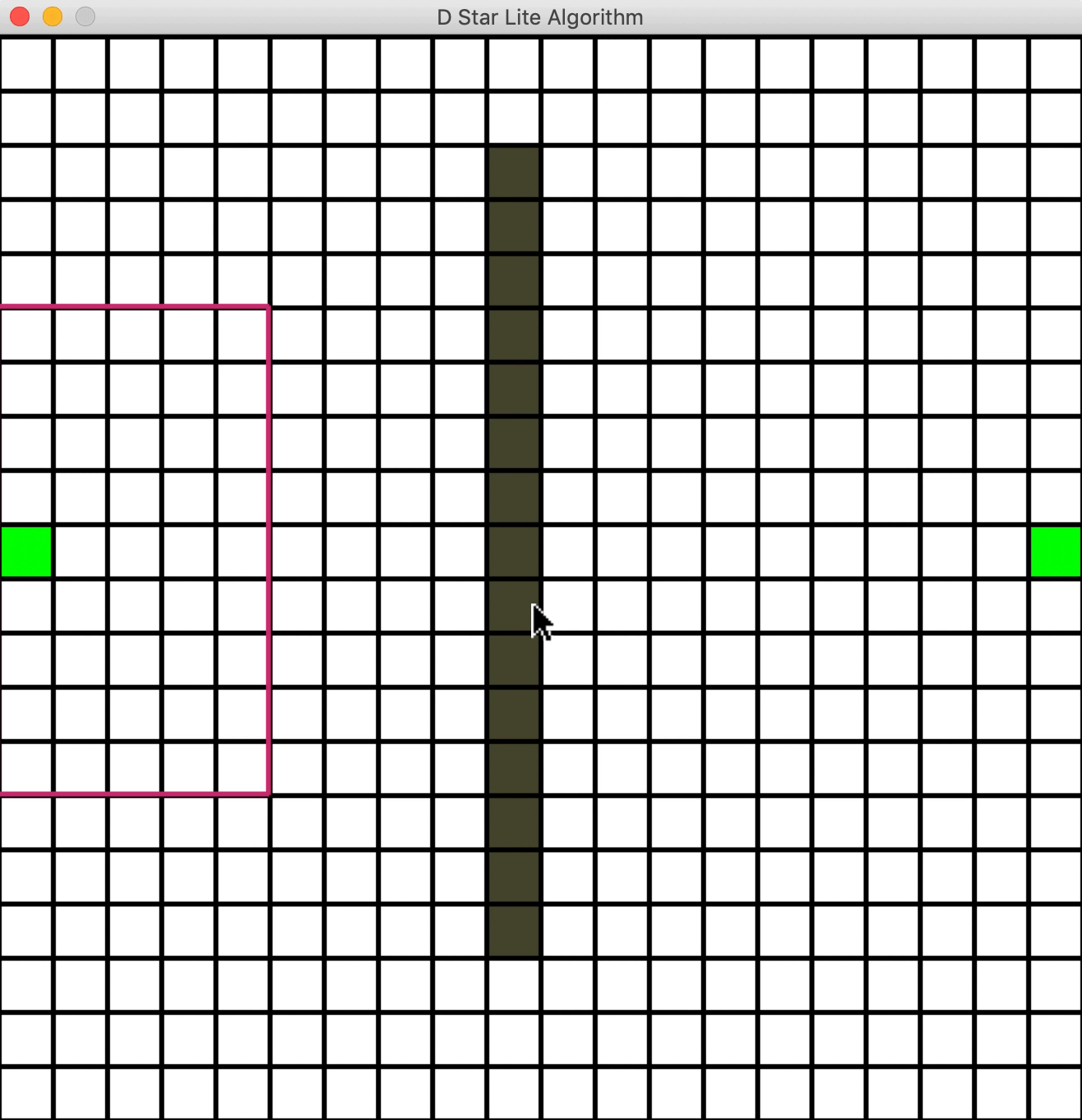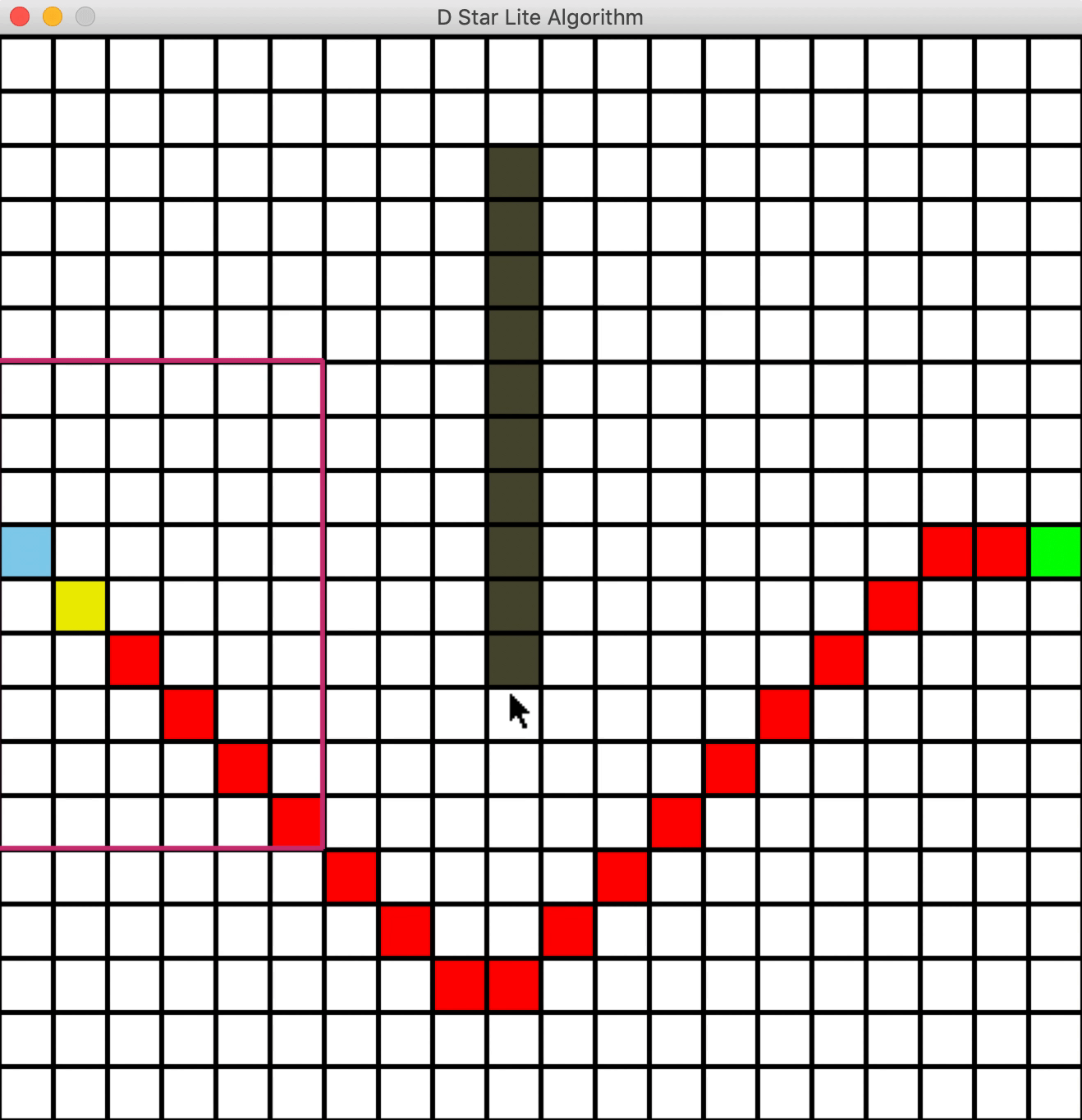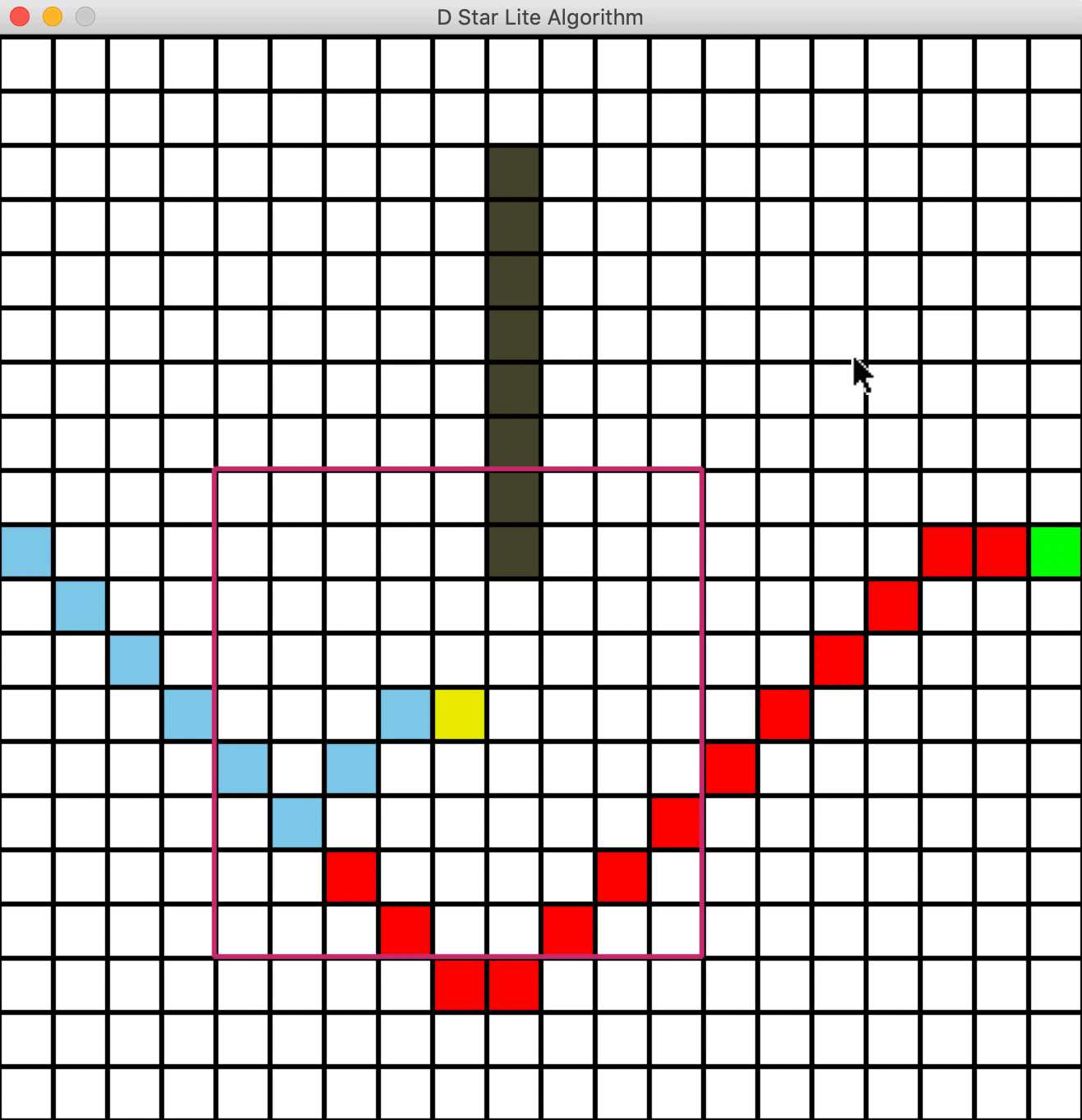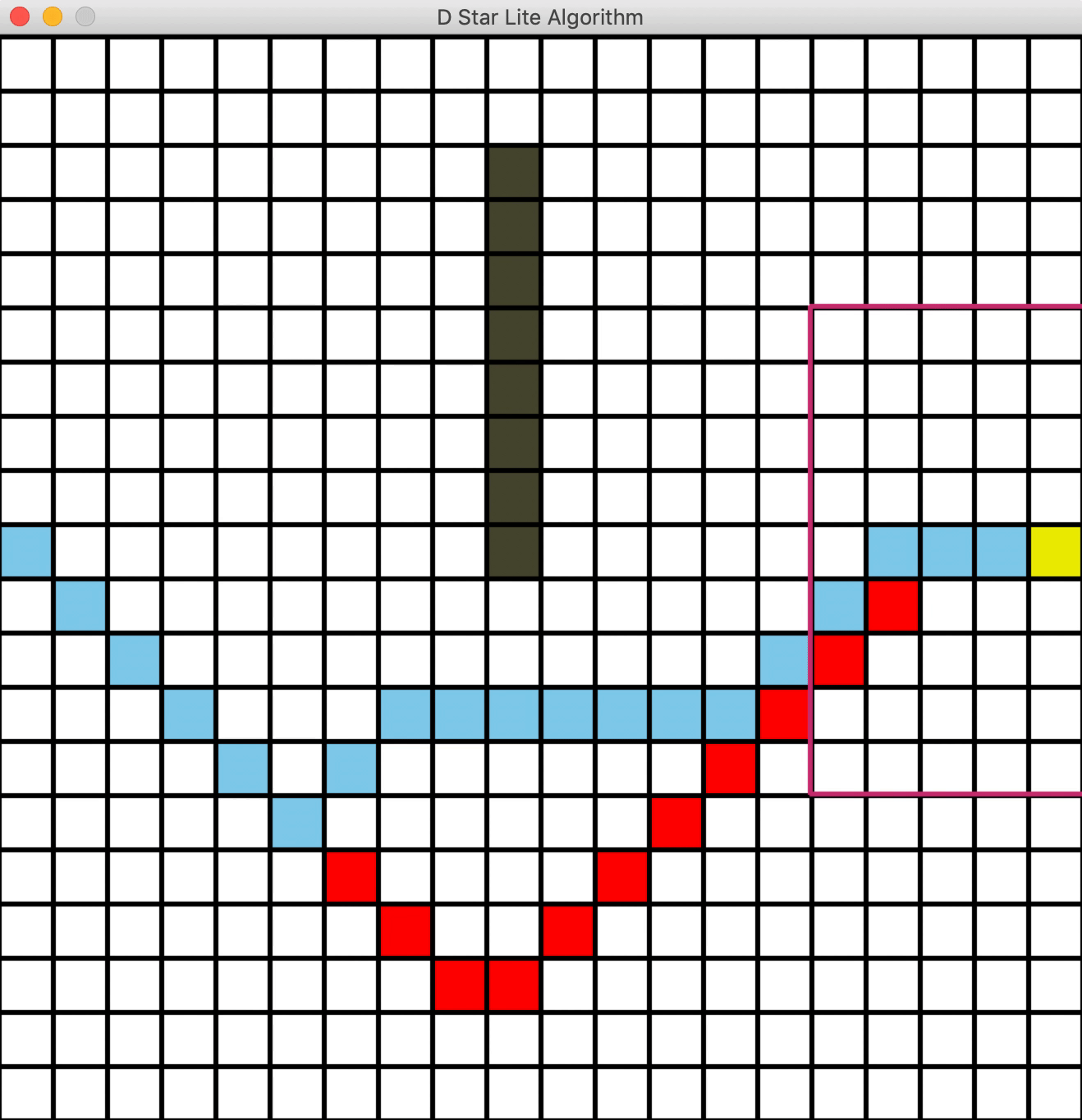
一个问题
一个遇到的问题就是:论文中并没给出父代节点和子代节点的明确定义,但是经过测试如果全部都用领域节点的话是可以得到正确结果的。
参考资料
一个A*算法的介绍博客:
https://paul.pub/a-star-algorithm/
D*算法介绍博客:
https://blog.csdn.net/lqzdreamer/article/details/85055569
D* Lite算法论文:
https://www.aaai.org/Papers/AAAI/2002/AAAI02-072.pdf
D* Lite算法介绍博客:
https://blog.csdn.net/lqzdreamer/article/details/85108310